El Cifrado de Hill
El cifrado de Hill es un método de cifrado de bloque que utiliza matrices para cifrar y descifrar mensajes. Es un método de cifrado simétrico, lo que significa que la misma clave se utiliza tanto para cifrar como para descifrar el mensaje.
Lester Hill
Matemático norteamericano que propone en el año 1929 el uso de matrices para la cifra de dos o más letras del texto en claro Hill patenta su invento con claves de 6 letras, pero como dicha clave debe ser fija para cada máquina, no puede competir con otras máquinas de la época como Enigma, Lorenz o Purple
Procedimiento de cifrado
Para cifrar un mensaje con el cifrado de Hill, primero se divide el mensaje en bloques de tamaño n, donde n es el tamaño de la matriz de cifrado. Cada bloque se representa como un vector de n elementos. A continuación, se multiplica cada vector por la matriz de cifrado utilizando la regla de multiplicación de matrices. El resultado es otro vector de tamaño n que representa el mensaje cifrado.
Para descifrar el mensaje, se realiza el mismo proceso, pero en lugar de utilizar la matriz de cifrado se utiliza su inversa. La inversa de una matriz es una matriz que, cuando se multiplica por la matriz original, produce la matriz identidad.
Es importante tener en cuenta que la matriz de cifrado debe cumplir ciertas propiedades para que el cifrado de Hill sea seguro. En particular, la matriz debe ser invertible y debe tener un tamaño adecuado (por lo general, se utilizan matrices de 2×2 o 3×3). Además, la clave de cifrado debe ser mantenida en secreto para evitar que los mensajes puedan ser descifrados por personas no autorizadas.

Desarollo
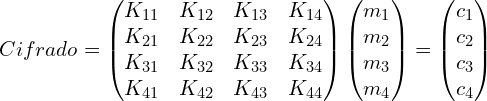
Algoritmo de mutiplicación.
* ![]()
* ![]()
* ![]()
* ![]()
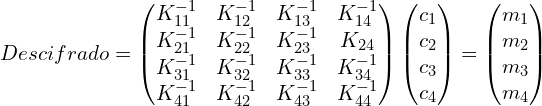
Condiciones Matriz Clave
* La matriz clave K debe tener inversa ![]() en el módulo de cifra n
en el módulo de cifra n
* Como ![]() mod n, en donde ADJ(K) es la matriz adjunta,
mod n, en donde ADJ(K) es la matriz adjunta, ![]() es la transpuesta y |K| el determinante. Este último valor |K| no podrá ser cero ni tener factores en común con n (condición de inversos)
es la transpuesta y |K| el determinante. Este último valor |K| no podrá ser cero ni tener factores en común con n (condición de inversos)
* Si el texto en claro no es múltiplo del bloque de N letras, el último bloque se rellenará con una letra predeterminada de poco uso
Hagamos un ejemplo.
* Usaremos una matriz de 4×4 que cumpla con las condiciones antes explicadas. Por ejemplo
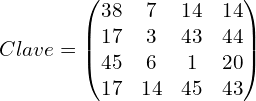
El determinante es: 288470
El determinante en mod(27) es: 2
Clave valida
* El mensaja a cifrar será: atacaremos al amanecer
* Haremos el digrama del mensaje en función a la dimensión de mi clave, en este caso 4
[ATAC][AREM][OSAL][AMAN][ECERX]. Rellenamos con una X si fuera necesario y suprimimos espacios en blanco
Cada digrama es un vector con la dimensión de la clave en ![]()
La estructura queda:
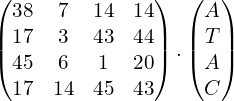
Relacionamos cada palabra del digrama con el valor correspondiente del alfabeto.
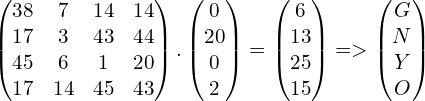
Desciframos
Usamos la clave para calcular la adjunta de la clave

Para sacar la matrix inversa de K, debemos multiplicar cada valor de la matriz **traspuesta** por el inverso de su determinante en modulo 27. Por lo tanto **el inverso de 2 en modulo 27 es 14**

Una vez que tenemos la matriz inversa podemos descifrar el mensaje:
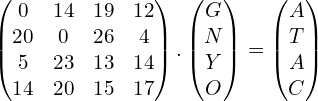
Fortaleza de la clave
Si n = primo, el número de matrices válidas K tiende al máximo ![]()
Ejemplo
Si hacemos una cifra con bloques de 8 letras (n=8= y usamos como módulo p = 29 (por ejemplo las mayúsculas y los signos +y -), el número de matrices válidas K= ![]() .Este espacio de claves será muy superior (254 veces mayor) a la del algoritmo AES 256, que tiene
.Este espacio de claves será muy superior (254 veces mayor) a la del algoritmo AES 256, que tiene ![]() claves posibles .Si p = 191 (un subconjunto imprimible del código ASCII), con un bloque de 8 caracteres, el número de matrices válidas se eleva a K=
claves posibles .Si p = 191 (un subconjunto imprimible del código ASCII), con un bloque de 8 caracteres, el número de matrices válidas se eleva a K= ![]() .Pero este sistema será muy vulnerable ante un criptoanálisis por texto en claro conocido, mediante el método de Gauss-Jordan
.Pero este sistema será muy vulnerable ante un criptoanálisis por texto en claro conocido, mediante el método de Gauss-Jordan
Romper Cifrado de Hill
Vectores unitarios
Se conoce como vector unitario a la fila de una matriz que contiene un uno en la columna que le corresponde en una matriz identidad y los demás valores son ceros.
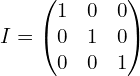
Si un bloque de texto se cifra con una matriz identidad, es decir con los vectores unitarios, se obtiene el mismo texto en claro
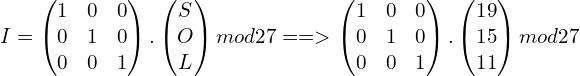
![]() <br>
<br>![]() <br>
<br>![]() <br>
<br>
Si la matriz clave K es de 2×2 no es tan difícil encontrar los vectores unitarios **AB (0 1)** y **BA (1 0)** en el texto en claro.
Veamos en ejemplo:
* Texto a cifrar: M=»ES OS AV IO NE SV OL **AB** AN MU YA **BA** JO»
* Texto cifrado: C=»WB YV NY ÑJ QV ÑV II **SV** EP GU HG **KX** XG»
* clave 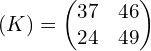
Por lo tanto si sabemos que AB se cifra como SV, podremos conocer ![]()
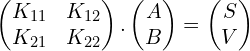
Si ![]() <br>
<br>![]() <br>
<br>![]()
Si ![]() <br>
<br>![]() <br>
<br>![]()
El siguiente paso es que si sabemos que BA se cifra como KX, podremos conocer ![]()
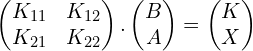
Si ![]() <br>
<br>![]() <br>
<br>![]()
Si ![]() <br>
<br>![]() <br>
<br>![]()
Resolvemos la clave
clave 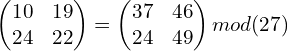
Recordar que las matemáticas se pueden contextualizar en «situaciones de aprendizaje» muy motivadoras y cercanas a la realidad.